معرفی و آموزش روش AHP

روش AHP یا همان فرآیند تحلیل سلسله مراتبی (Analytical Hierarchy Process) از جامعترین مدلهای تصمیمگیری با معیارهای چندگانه است که در این مطلب به معرفی و آموزش آن پرداخته شده است.
تاریخچه روش AHP
در ارزیابی هر موضوعی ما نیاز به معیار اندازهگیری با شاخص داریم، انتخاب شاخص مناسب به ما امكان میدهد كه مقایسه درستی بین گزینهها یا آلترناتیوها به عمل آوریم. اما وقتی كه چند یا چندین شاخص برای ارزیابی در نظر گرفته میشود، كار ارزیابی پیچیده میكند و پیچیدگی كار زمانی بالا میگیرد كه معیارهای چندگانه باهم در فضا و از جنسهای مختلف باشند. در این هنگام كار ارزیابی و مقایسه از حالت ساده تحلیلی كه ذهن قادر به انجام آن است خارج میشود و به یك ابزار تحلیل عملی قوی نیاز خواهد بود.
در هر تصمیمگیری فضای تصمیمسازی به صورت پیوسته یا گسسته است. همچنین ممکن است تصمیمگیری تکمعیاره یا چندمعیاره باشد، بعلاوه این معیارها می توانند به صورتهای کمی، کیفی و یا تلفیقی از هر دو (در حالت چندمعیاره) باشند که در هریک از این حالتها نحوه تصمیمگیری متفاوت است. در نمودار زیر انواع تصمیمگیری نشان داده شده است.
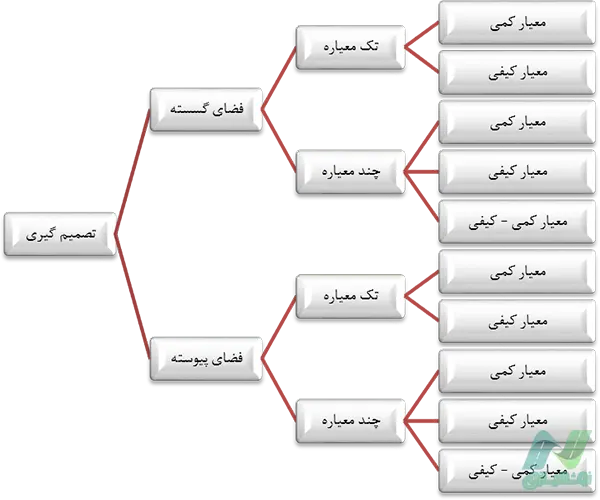
در فضای گسسته و حالت تکمعیاره تصمیمگیری راحت است. فرض کنید از بین دو مسیر میخواهیم مسیر کوتاهتر را انتخاب کنیم (معیار کمی). بدین منظور کافی است که یک واحد برای اندازهگیری طول تعریف کرده و هر دو مسیر را براساس آن بسنجیم. ولی در حالتی که معیار به صورت کیفی باشد، تصمیمگیری مقداری مشکل بوده و لازم است که ابتدا استاندارد تعریف شود. بهطور مثال چنانچه بخواهیم از بین چند اتومبیل زیباترین را انتخاب کنیم، ابتدا باید زیبایی را برای اتومبیل تعریف نموده و سپس اقدام به رتبهبندی نماییم.
در حالتی که معیارهای چندگانه (اعم از کیفی و کمی) مطرح باشند، علاوه بر مشکل فوق، مسأله تبدیل معیارها به یکدیگر نیز مطرح است. بنابراین گفته میشود که فرآیند تصمیمگیری چند معیاره با دو مشکل اساسی روبهرو است:
- فقدان استاندارد برای اندازهگیری معیارهای کیفی
- فقدان واحد برای تبدیل معیارها (اعم از کمی و کیفی) به یکدیگر
با توجه به مشکلات مربوط به فرآیند تصمیمگیری با معیارهای چندگانه، می توان گفت که در این حالت تصمیمگیری ساده نبوده و بعلت عدم وجود استاندارد از سرعت و دقت تصمیمگیری به مقدار زیادی کاسته شده و باعث میشود که فرآیند تصمیمگیری به مقدار زیادی به فرد تصمیمگیرنده وابسته باشد. برای رفع این مشکل و یا حداقل کردن آثار جانبی آن، روشهای تصمیمگیری با معیارهای چندگانه طراحی شدهاند که هر کدام از قوانین و اصول خاصی پیروی کرده و دارای مزایا و معایبی هستند.
فورمن معتقد است که یک سیستم پشتیبانی تصمیمگیری چندمعیاره باید دارای خصوصیات زیر باشد:
- امکان فرموله کردن مساله و تجدیدنظر در آن را بدهد.
- گزینههای مختلف را در نظر بگیرد.
- معیارهای مختلف را (که عموماً در تضاد نیز هستند) درنظر بگیرد.
- معیارهای کمی وکیفی را در تصمیمگیری دخالت دهد.
- نظرات افراد مختلف را در مورد گزینهها و معیارها لحاظ کند.
- امکان تلفیق قضاوتها برای محاسبه نرخ نهایی را بدهد.
- بر مبنای یک تئوری قوی استوار باشد.
روشهای ارزیابی چندمعیاری از دهه 1980 به این طرف ابداع و مورد توجه قرار گرفتهاند. از بین روشهای ارزیابی چندمعیاری متعددی كه در سالهای اخیر در زمینههای گوناگون مورد استفاده قرار گرفتهاند، از جمله تحلیل سیستم، تئوری مطلوبیت چند مشخصه، تصمیمگیری چندمعیاری، تئوری قضاوت اجتماعی، روش ارزیابی چندمعیاری فرآیند تحلیل سلسله مراتبی AHP و …
فرآیند تحلیل سلسله مراتبی (Analytical Hierarchy Process) در اواخر دهه 1970 توسط توماس الساعتی معرفی شده است که یکی از جامعترین سیستمهای طراحی شده برای تصمیمگیری با معیارهای چندگانه است. زیرا امکان ترکیب معیارهای کیفی و کمی را به طور همزمان میسر ساخته و به محاسبه میزان اهمیت معیارها به صورت کمی میپردازد.
معرفی روش AHP
روش AHP یکی از معروفترین فنون تصمیمگیری چندمعیاره (Multi Criteria Decision Making) است. این روش با استفاده از ماتریسهای مقایسه دو به دو به مقایسهی گزینههای مختلف نسبت به یکدیگر پرداخته و در نهایت ارجحترین گزینه را انتخاب میکند. برای چنین گزینهای نیاز به جمعآوری اطلاعات از تصمیمگیرندگان و کارشناسان داریم. این امر به تصمیمگیرنده امکان میدهد که فارغ از هرگونه نفوذ و مزاحمت خارجی تنها روی مقایسه دو به دویی تمرکز کند.
روش AHP روشی است منعطف، قوی و ساده برای تصمیمگیری در شرایطی که معیارهای تصمیمگیری متضاد، انتخاب بین گزینهها را با مشکل مواجه میسازد و باید تصمیمگیری در یک فضای چندبعدی صورت پذیرد.
این روش به دلیل بنا نهاده شدن بر روی مقایسات زوجی، قضاوت و محاسبات را تسهیل نموده و همچنین میتواند میزان سازگاری و ناسازگاری تصمیم را نشان دهد. از روش AHP میتوان برای کاربردهای مختلفی استفاده نمود:
- انتخاب: انتخاب یک گزینه از میان مجموعهای از گزینهها براساس چندین معیار
- رتبهبندی: قرار دادن مجموعهای از گزینهها به ترتیب از بالاترین اولویت تا پایینترین
- تخصیص منبع: تخصیص دادن منابع به مجموعهای از گزینهها
- بهینه کاوی: مقایسه روالها در یک سازمان با سازمانهای مشابه با کیفیت بالاتر
- مدیریت کیفیت: سروکار داشتن با جنبههای چندبعدی کیفیت و بهبود آن
باتوجه به اینكه اغلب مسائل و موضوعات مربوط به شهرسازی از طریق شاخصهای كیفی و كمی قابل بررسی هستند که از قابلیتهای روش AHP است، این مدل میتواند به عنوان یکی از ابزارهای قوی برای تحلیل مسائل شهرسازی استفاده شود. انعطافپذیری، سادگی محاسبات و امكان رتبهبندی نهائی گزینهها نیز از مزیتهای دیگر روش AHP هستند كه میتوانند كمك مؤثری در بررسیهای مربوط به مسائل شهری و برنامهریزی شهری و منطقهای باشند و میتواند کاربرهای مختلفی در حوزه شهرسازی داشته باشند که برخی از آنها عبارتند از:
- کاربرد این مدل در بحث مکانیابیهای شهری از اهمیت قابل توجهی برخوردار میباشد. مکانیابی صنایع، کارخانجات، دفع مواد زائد، بازار شهری، مکانیابی شهرهای جدید و انتخاب مکان پایتخت جدید و …
- کارایی جهت ارزیابی طرحها و برنامهریزی استراتژیک
- کاربرد در بحث توسعه فضایی و فیزیکی و…
نرمافزارهای مختلفی برای انجام تحلیل AHP طراحی شده است که از جمله آنها میتوان به نرم افزار Expert Choice و Super Decision اشاره کرد. همچنین در محیط GIS نیز با استفاده از اکستنشن طراحی شده توسط O.Marinoni مخصوص این نرمافزار که با عنوان extAhp میباشد، میتوان روش AHP را در GIS نیز پیادهسازی کرد.
آموزش روش AHP
پیادهسازی روش AHP در یک تصمیمگیری شامل 5 فاز میباشد:
1- ساختن سلسله مراتبی
اولین قدم در فرآیند تحلیل سلسله مراتبی، تعیین عواملی است که در تصمیمگیری مهم میباشند و میبایست این عوامل را در قالب یک درخت تصمیمگیری به صورت سلسله مراتبی بیان کنیم. در این درخت تصمیمگیری باید هدف، معیارها و گزینهها و ارتباط بین آنها نشان داده شود. تبدیل موضوع یا مسئله مورد بررسی به یك ساختار سلسلهمراتبی مهمترین قسمت روش AHP محسوب میشود. زیرا در این قسمت با تجزیه مسائل مشكل و پیچیده، فرآیند تحلیل سلسله مراتبی آنها را به شكلی ساده كه با ذهن و طبیعت بشری مطابقت دارد تبدیل میكند.
فرض کنید سه سایت A، B و C به عنوان گزینههای موردنظر برای مکانیابی مشخص شدهاند. قرار است سایت مناسب جهت احداث مدرسه براساس معیارهای هزینه، دسترسی، کاربریهای همجوار و موقعیت استقرار انتخاب شود. معیار هزینه به دو زیرمعیار قیمت زمین و مالکیت، معیار دسترسی به سه زیرمعیار دسترسی به معابر اصلی و فرعی، دسترسی پیاده و دوچرخه و دسترسی به ایستگاه حملونقل عمومی، موقعیت استقرار به دو زیرمعیار مساحت زمین و انطباق با طرح مصوب تقسیم میشوند. نمودار این ساختار سلسله مراتبی به صورت زیر است:

2- وزندهی معیارها و زیرمعیارها
برای تعیین ضریب اهمیت (وزن) معیارها و زیرمعیارها، دو به دو آنها را مقایسه میكنیم، مبنای قضاوت در این امر مقایسه جدول مقیاس کمیتی زیر است كه بر اساس آن و با توجه به هدف بررسی، شدت برتری معیار i نسبت به معیار j تعیین میشود و تمامی معیارها دوبه دو با هم مقایسه میشوند.
| امتیاز | تعریف | توضیح |
|---|---|---|
| 1 | اهمیت مساوی | در تحقق هدف دو معیار اهمیت مساوی دارند. |
| 3 | اهمیت اندکی بیشتر | تجربه نشان میدهد که برای تحقق هدف، اهمیت i اندکی بیشتر از j است. |
| 5 | اهمیت بیشتر | تجربه نشان میدهد که اهمیت i بیشتر از j است. |
| 7 | اهمیت خیلی بیشتر | تجربه نشان میدهد که اهمیت i خیلی بیشتر از j است. |
| 9 | اهمیت مطلق | اهمیت خیلی بیشتر i نسبت به j به طور قطعی به اثبات رسیده است. |
| 2,4,6,8 | مقادیر مابین | هنگامی که حالتهای میانه وجود دارد. |
در این مقایسات و تعیین ضریب اهمیت چهار اصل وجود دارد که میبایست به آنها توجه شود:
- شرط معکوس (Reverse conditions): اگر ترجیح عنصر A بر B برابر با N باشد، ترجیح عنصر B بر عنصر A برابر 1/N میباشد.
- اصل همگنی (Homogeneity): عنصر A با B باید همگن و قابل مقایسه باشند و برتری عنصر A بر B نمیتواند بینهایت و صفر باشد.
- اصل وابستگی (Dependency): هر عنصر سلسله مراتبی بر عنصر سطح بالاتر خود وابسته باشد و به صورت خطی این وابستگی تا بالاترین سطح میتواند ادامه داشته باشد.
- اصل انتظارات (Expectations): هرگاه تغییری در ساختمان سلسله مراتبی رخ دهد، پروسه ارزیابی باید مجدد انجام گیرد.
در فرآیند سلسله مراتبی عناصر هر سطح نسبت به عنصر مربوطه خود در سطح بالاتر به صورت زوجی مقایسه شده و وزن آنها محاسبه میگردد که این وزنها را وزن نسبی مینامند. سپس با تلفیق وزنهای نسبی، وزن نهایی هر گزینه مشخص میگردد که آن را وزن مطلق مینامند. سپس وزن معیارها نیز نسبت به هدف تعیین شده و با ترکیب آنها وزن نهایی گزینهها مشخص میگردد.
چهار روش تقریبی مجموع سطری، مجموع ستونی، میانگین حسابی و میانگین هندسی برای تعیین ضریب اهمیت توسط الساعتی معرفی شده است که روش میانگین هندسی به دلیل دقت بیشتر، مورد استفاده قرار میگیرد. برای این منظور میانگین هندسی ردیفهای هر ستون محاسبه میشود. سپس جهت نرمالیزه کردن، هر میانگین هندسی را بر مجموع میانگینهای هندسی تقسیم میکنیم.
به این ترتیب جداول مقایسه دودویی معیارها و زیرمعیارها و وزن نسبی هریک از آنها برای مثال فوق، به شرح زیر میباشد:
| مقایسه دودویی اهمیت معیارها | ||||||
| معیار | هزینه | دسترسی | کاربریهای همجوار | موقعیت استقرار | میانگین هندسی | وزن نسبی |
| هزینه | 1 | 1/2 | 3 | 1/3 | 0.84 | 0.17 |
| دسترسی | 2 | 1 | 4 | 1/2 | 1.41 | 0.29 |
| کاربریهای همجوار | 1/3 | 1/4 | 1 | 1/5 | 0.36 | 0.07 |
| موقعیت استقرار | 3 | 2 | 5 | 1 | 2.34 | 0.47 |
| جمع | 4.95 | 1 | ||||
| مقایسه دودویی اهمیت زیرمعیارهای هزینه | ||||
| معیار | قیمت زمین | مالکیت | میانگین هندسی | وزن نسبی |
| قیمت زمین | 1 | 1/3 | 0.57 | 0.25 |
| مالکیت | 3 | 1 | 1.73 | 0.75 |
| جمع | 2.3 | 1 | ||
| مقایسه دودویی اهمیت زیرمعیارهای دسترسی | |||||
| معیار | معابر اصلی و فرعی | مسیر پیاده و دوچرخه | حمل و نقل عمومی | میانگین هندسی | وزن نسبی |
| معابر اصلی و فرعی | 1 | 3 | 5 | 2.47 | 0.64 |
| مسیر پیاده و دوچرخه | 1/3 | 1 | 3 | 1 | 0.26 |
| حمل و نقل عمومی | 1/5 | 1/3 | 1 | 0.4 | 0.1 |
| جمع | 3.87 | 1 | |||
| مقایسه دودویی اهمیت زیرمعیارهای موقعیت استقرار | ||||
| معیار | مساحت | انطباق با طرح مصوب | میانگین هندسی | وزن نسبی |
| مساحت | 1 | 2 | 1.41 | 0.67 |
| انطباق با طرح مصوب | 1/2 | 1 | 0.71 | 0.33 |
| جمع | 2.12 | 1 | ||
3- تعیین ضریب اهمیت گزینهها
در مرحله سوم از روش AHP به وزندهی گزینهها پرداخته خواهد شد. در این مرحله، ارجحیت هر یک از گزینهها در ارتباط با هریک از زیرمعیارها، و اگر زیر معیاری نداشته باشد، مستقیماً با خود آن معیار، مورد قضاوت و داوری قرار میگیرد. مبنای این قضاوت نیز مشابه وزندهی معیارها، همان جدول مقیاس کمیتی است. فقط در این مرحله مهمتر بودن گزینه ملاک نیست، ارجح بودن گزینه و مقدار ارجحیت مطرح است. در نتیجه جدول مقیاس کمیتی به شرح زیر خواهد شد:
| امتیاز (شدت ارجحیت) | تعریف |
|---|---|
| 1 | ترجیح یکسان (Equally Preferred) |
| 3 | کمی مرجح (Moderately Preferred) |
| 5 | ترجیح بیشتر (Strongly Preferred) |
| 7 | ترجیح خیلی بیشتر (Very Strongly Preferred) |
| 9 | کاملا مرجح (Extremely Preferred) |
| 2و4و6و8 | ترجیحات بینابین (وقتی حالتهای میانه وجود دارد) |
فرآیند مقایسه دقیقا مشابه با مرحله قبلی بر مبنای ماتریس مقایسه دودویی معیارها یا گزینهها میباشد و از طریق نرمالیزه کردن میانگین هندسی ردیفهای این ماتریسها، ضرایب اهمیت گزینهها بدست خواهد آمد. باید به یک تفاوت عمده در این مقایسه اشاره شود. مقایسه گزینههای مختلف نسبت به زیرمعیارها و یا معیارها (اگر معیاری، زیرمعیار نداشته باشد) صورت میپذیرد. در صورتی که مقایسه معیارها با یکدیگر نسبت به هدف مطالعه صورت میپذیرد.
جداول مقایسه دودویی گزینهها با هریک از معیارها و زیرمعیارها در مثال فوق به شرح زیر میباشد:
| مقایسه دودویی گزینهها نسبت به معیار قیمت زمین | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 3 | 4 | 2.29 | 0.62 |
| سایت B | 1/3 | 1 | 2 | 0.87 | 0.24 |
| سایت C | 1/4 | 1/2 | 1 | 0.5 | 0.14 |
| جمع | 3.66 | 1 | |||
| مقایسه دودویی گزینهها نسبت به معیار مالکیت | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 1/3 | 1 | 0.69 | 0.2 |
| سایت B | 3 | 1 | 3 | 2.08 | 0.6 |
| سایت C | 1 | 1/3 | 1 | 0.69 | 0.2 |
| جمع | 3.46 | 1 | |||
| مقایسه دودویی گزینهها نسبت به معیار دسترسی به معابر اصلی و فرعی | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 3 | 2 | 1.82 | 0.54 |
| سایت B | 1/3 | 1 | 1/2 | 0.55 | 0.16 |
| سایت C | 1/2 | 2 | 1 | 1 | 0.3 |
| جمع | 3.37 | 1 | |||
| مقایسه دودویی گزینهها نسبت به معیار دسترسی به مسیر پیاده و دوچرخه | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 1/4 | 1/3 | 0.44 | 0.12 |
| سایت B | 4 | 1 | 2 | 2 | 0.56 |
| سایت C | 3 | 1/2 | 1 | 1.14 | 0.32 |
| جمع | 3.58 | 1 | |||
| مقایسه دودویی گزینهها نسبت به معیار دسترسی به حمل و نقل عمومی | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 5 | 3 | 2.47 | 0.64 |
| سایت B | 1/5 | 1 | 1/3 | 0.4 | 0.1 |
| سایت C | 1/3 | 3 | 1 | 1 | 0.26 |
| جمع | 3.87 | 1 | |||
| مقایسه دودویی گزینهها نسبت به معیار دسترسی به کاربریهای همجوار | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 2 | 1/3 | 0.87 | 0.24 |
| سایت B | 1/2 | 1 | 1/4 | 0.5 | 0.14 |
| سایت C | 3 | 4 | 1 | 2.29 | 0.62 |
| جمع | 3.66 | 1 | |||
| مقایسه دودویی گزینهها نسبت به معیار مساحت زمین | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 1/2 | 1/3 | 0.55 | 0.16 |
| سایت B | 2 | 1 | 1/2 | 1 | 0.3 |
| سایت C | 3 | 2 | 1 | 1.82 | 0.54 |
| جمع | 3.37 | 1 | |||
| مقایسه دودویی گزینهها نسبت به معیار انطباق با طرح مصوب | |||||
| معیار | سایت A | سایت B | سایت C | میانگین هندسی | وزن نسبی |
| سایت A | 1 | 1/3 | 3 | 0.4 | 0.26 |
| سایت B | 3 | 1 | 5 | 2.47 | 0.64 |
| سایت C | 1/3 | 1/5 | 1 | 1 | 0.1 |
| جمع | 3.87 | 1 | |||
4- تعیین امتیاز نهایی و اولویتبندی گزینهها
در چهارمین مرحله از روش AHP به تلفیق ضرایب به دست آمده از مراحل قبلی پرداخته میشود. برای این کار از اصل ترکیب سلسلهمراتبی ساعتی که منجر به یک بردار اولویت با درنظرگرفتن همه قضاوتها در تمامی سطوح سلسلهمراتبی می شود، استفاده خواهد شد:
![]()
که در آن:
wk: ضریب اهمیت معیار k
wi: ضریب اهمیت زیر معیار i
gij: امتیاز گزینه j در ارتباط با زیر معیار i
به زبان سادهتر وزن نهایی زیرمعیار که به صورت سلسله مراتبی از ضرب ضریب اهمیت زیرمعیار در ضریب اهمیت معیار بالادستی بدست میآید را در وزن گزینه موردنظر در زیرمعیار ضرب مینماییم. از جمع وزنهای نهایی که از این روش برای هر گزینه بدست میآید، وزن نهایی گزینه بدست آمده و میتوان به اولویتبندی گزینهها پرداخت.
به عنوان مثال وزن سایت A برای زیرمعیار قیمت زمین از ضرب وزن نسبی معیار و زیرمعیار و گزینه به صورت زیر بدست خواهد آمد.
وزن نهایی سایت A در زیرمعیار قیمت زمین = 0.17×0.25×0.62 = 0.02635
در مثال بررسی شده مطابق نمودار و جدول زیر وزن نهایی برای هر گزینه بدست خواهد آمد.
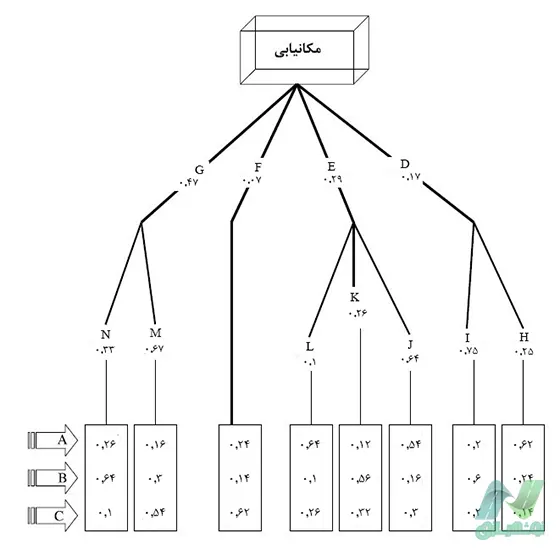
| گزینهها | سایت A | سایت B | سایت C | |
| هزینه D | قیمت زمین H | 0.02635 | 0.0102 | 0.00595 |
| مالکیت I | 0.0255 | 0.0765 | 0.0255 | |
| دسترسی E | معابر اصلی و فرعی J | 0.100224 | 0.029696 | 0.05568 |
| مسیر پیاده و دوچرخه K | 0.009048 | 0.042224 | 0.024128 | |
| حمل و نقل عمومی L | 0.01856 | 0.0029 | 0.00754 | |
| کاربریهای همجوار F | 0.0168 | 0.0098 | 0.0434 | |
| موقعیت استقرار G | مساحت زمین M | 0.050384 | 0.09447 | 0.170046 |
| انطباق با طرح مصوب N | 0.040326 | 0.099264 | 0.01551 | |
| امتیاز نهایی | 0.287192 | 0.365054 | 0.347754 | |
مطابق تحلیل انجام شده به روش AHP باتوجه به اینکه سایت B بیشترین امتیاز را کسب نمود، بهترین گزینه برای احداث مدرسه میباشد.
5- بررسی سازگاری قضاوتها
یکی از مزیتهای روش AHP امکان بررسی سازگاری قضاوتها و مقایسههای انجام شده است. برای این منظور از ضریب ناسازگاری (Inconsistency Ratio (I.R)) استفاده میشود که از تقسیم شاخص ناسازگاری (Inconsistency Index (I.I)) به شاخص تصادفی بودن (Random Index (R.I)) بدست میآید.
محدوده سازگاری به تصمیمگیرنده بستگی دارد، اما در حالت کلی، چنانچه این ضریب کوچکتر یا مساوی 0.1 باشد، سازگاری در قضاوتها مورد قبول است، در غیر اینصورت باید در قضاوتها تجدیدنظر صورت گیرد. به عبارت دیگر ماتریس مقایسه دودویی معیارها باید مجدداً تشکیل شود.
![]()
در روش میانگین هندسی که یک روش تقریبی است، به جای محاسبه مقدار ویژه ماکزیمم (λmax) از L به شرح زیر استفاده میشود:
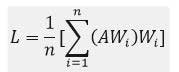
که در آن AWi برداری است که از ضرب ماتریس مقایسه دودویی معیارها در بردار Wi (بردار وزن یا ضریب اهمیت معیارها) به دست میآید. بررسی سازگاری قضاوتها در ماتریس دودویی معیارها حاکی از آن است که سازگاری در قضاوت رعایت شده است.
شاخص تصادفی بودن با توجه به تعداد معیارها (n) از جدول زیر قابل استخراج است:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| I.I.R | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 | 1.51 | 1.48 | 1.56 | 1.57 | 1.59 |
این جدول به این شکل بدست آمده است که ماتریسهای مقایسات زوجی، به شکل رندوم با ابعاد ماتریسی مختلف تولید شده و سپس نرخ سازگاری آنها محاسبه میشود که باید دید آیا از حدود 0.1 کمتر هستند یا خیر.
باتوجه به زمانبر بودن بررسی تک تک نرخهای ناسازگاری که اغلب توسط نرمافزار انجام میشود، در مثال ارائه شده، یک مورد مربوط به محاسبه نرخ ناسازگاری زیرمعیارهای دسترسی را محاسبه میکنیم.
| زیرمعیار | معابر اصلی و فرعی | مسیر پیاده و دوچرخه | حمل و نقل عمومی | وزن نسبی |
| معابر اصلی و فرعی | 1 | 3 | 5 | 0.64 |
| مسیر پیاده و دوچرخه | 1/3 | 1 | 3 | 0.26 |
| حمل و نقل عمومی | 1/5 | 1/3 | 1 | 0.1 |
بردار مجموع وزنی (AW) دسترسی به معابر اصلی و فرعی = (1×0.64)+(3 ×.0.26)+(5×0.1) = 1.92
بردار مجموع وزنی (AW) دسترسی به مسیر پیاده و دوچرخه = (0.33×0.64)+(1×0.26)+(3×0.1) = 0.7712
بردار مجموع وزنی (AW) دسترسی به ایستگاه حمل و نقل عمومی = (0.2×0.64)+(0.33×0.26)+(1×0.1) = 0.3138

باتوجه به اینکه ضریب ناسازگاری برابر با 0.03 بوده و کمتر از 0.1 است، میتوان نتیجه گرفت که سنجش و مقایسه زوجی انجام شده برای این زیرمعیار سازگار است.
نتایج به دست آمده از این بررسی نشان میدهد كه روش AHP باتوجه به خصوصیات ویژه آن میتواند در بررسی موضوعات مربوط به برنامهریزی شهری و منطقهای کاربرد مطلوبی داشته باشد.
مزایا و معایب روش AHP
این فرآیند مجموعهای از قضاوتها (تصمیمگیریها) و ارزشگزاریهای شخصی به یک شیوه منطقی میباشد. بنابراین از یک طرف وابسته به تصورات شخصی و تجربه میباشد و از طرف دیگر به منطق، درک و تجربه جهت تصمیمگیری و قضاوت نهایی مربوط میشود. ساعتی، مزایای فرآیند تحلیل سلسله مراتبی را به شرح زیر بیان میکند:
- یگانگی و یکتایی مدل (Unity): فرآیند تحلیل سلسله مراتبی یک مدل یگانه، ساده و انعطاف پذیر برای حل محدوده وسیعی از مسائل بدون ساختار است که به راحتی قابل درک برای همگان میباشد.
- پیچیدگی (Complexity): برای حل مسائل پیچیده، روش AHP هم نگرش سیستمی و هم تحلیل جزء به جزء را به صورت توأم به کار میبرد. عموماً افراد در تحلیل مسائل یا کلنگری کرده و یا به جزئیات پرداخته و کلیات را رها میکنند. در حالی که فرآیند تحلیل سلسله مراتبی هر دو بعد را با هم به کار میبندد.
- همبستگی و وابستگی متقابل (Interdependence): فرآیند تحلیل سلسله مراتبی وابستگی را به صورت خطی در نظر میگیرد. ولی برای حل مسائلی که اجزاء به صورت غیر خطی وابستهاند نیز بهکار گرفته میشود.
- ساختار سلسله مراتبی (Hierarchy Structure): روش AHP اجزای یک سیستم را به صورت سلسله مراتبی سازماندهی میکند که این نوع سازماندهی با تفکر انسان تطابق داشته و اجزاء در سطوح مختلف طبقهبندی میشوند.
- اندازهگیری (Measurement): فرآیند تحلیل سلسله مراتبی مقیاسی برای اندازهگیری معیارهای کیفی تهیه کرده و روشی برای تخمین و برآورد اولویتها فراهم میکند.
- سازگاری (Consistency): روش AHP سازگاری منطقی قضاوتهای استفاده شده در تعیین اولویتها را محاسبه کرده و ارائه مینماید.
- تلفیق (Synthesis): فرآیند تحلیل سلسله مراتبی منجر به برآورد رتبه نهایی هر گزینه میشود.
- تعادل (Tradeoffs): روش AHP اولویتهای وابسته به فاکتورها در یک سیستم را در نظر گرفته و بین آنها تعادل برقرار میکند و فرد را قادر میسازد که بهترین گزینه را براساس اهدافش انتخاب کند.
- قضاوت و توافق گروهی (Judgment and Consensus): فرآیند تحلیل سلسله مراتبی بر روی توافق گروهی اصرار و پافشاری ندارد ولی تلفیقی از قضاوتهای گوناگون را میتواند ارائه نماید.
- تکرار فرآیند (Process Repetition): روش AHP فرد را قادر می سازد که تعریف خود را از یک مسئله تصحیح کند و قضاوت و تصمیم خود را بهبود دهند.
از جمله مهمترین معایب این روش به وابستگی این مدل به تجربه است و مقایسهها اغلب براساس تجربه است. در نتیجه ارزش نسبی به گزینهها و اعمال سلیقهها از معایب بزرگ کاربرد روش AHP در تحلیل مسائل شهری میباشد. در بعضی موارد نیز، امکان تبدیل به یک مجموعه سلسله مرتبی امکان پذیر نیست.
در پیوست 4 فایل پاورپوینت مختلف همراه با دو فایل PDF و یک فایل Word که در زمینه معرفی روش تحلیل سلسله مراتبی AHP هستند، ارائه شده است.